t-SNE (t-distributed stochastic neighbour embedding; van der Maaten & Hinton 2008) is a method of visualising high-dimensional data sets in low dimensions. It works by defining a set of probabilities that two points in high dimensional space are “similar” or “neighbours” based on a Gaussian kernel centered at each point. Then, the embedding into low (usually 2) dimensional space is chosen so that the similarities based on a \(t_1\) kernel are as close as possible to those in the high dimensional space. The fat-tailed \(t_1\) kernel stops the points from clumping up too much. One way of thinking about it is that the extra variance in the distribution makes up for the loss of dimensionality. Unlike PCA it’s nonlinear in distance. In effect, it clusters points so that the local structure is maintained more than the larger scale structure. The point that’s closest to you in high dimensions will probably still be closest to you in the embedding, but the point that’s furthest away from you won’t necessarily stay that way.
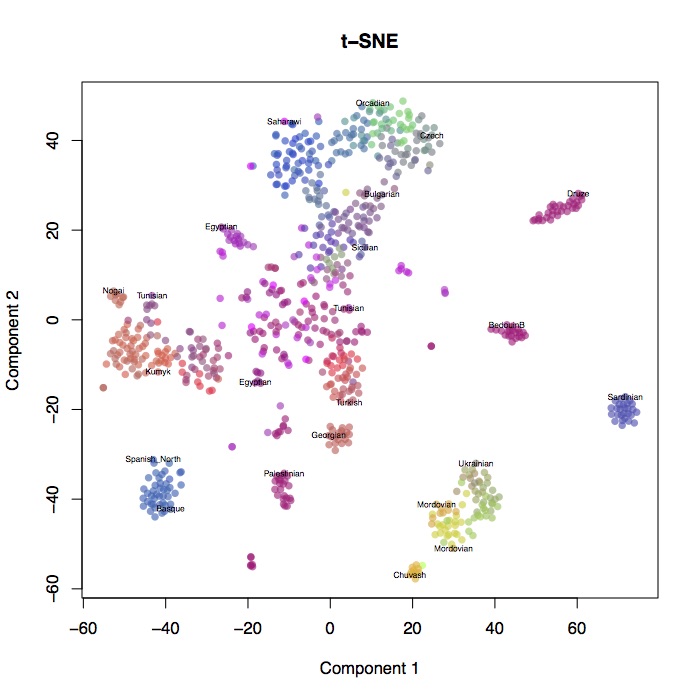
I ran t-SNE on the human origins dataset that I analysed here and here. I used the first 50 PC’s as input to the t-SNE algorithm (using the tsne package in R), weighted by the eigenvalues (although the weighting didn’t make much difference to the results). Shown above are the results, and below is the geographic structure and PCA for comparison.
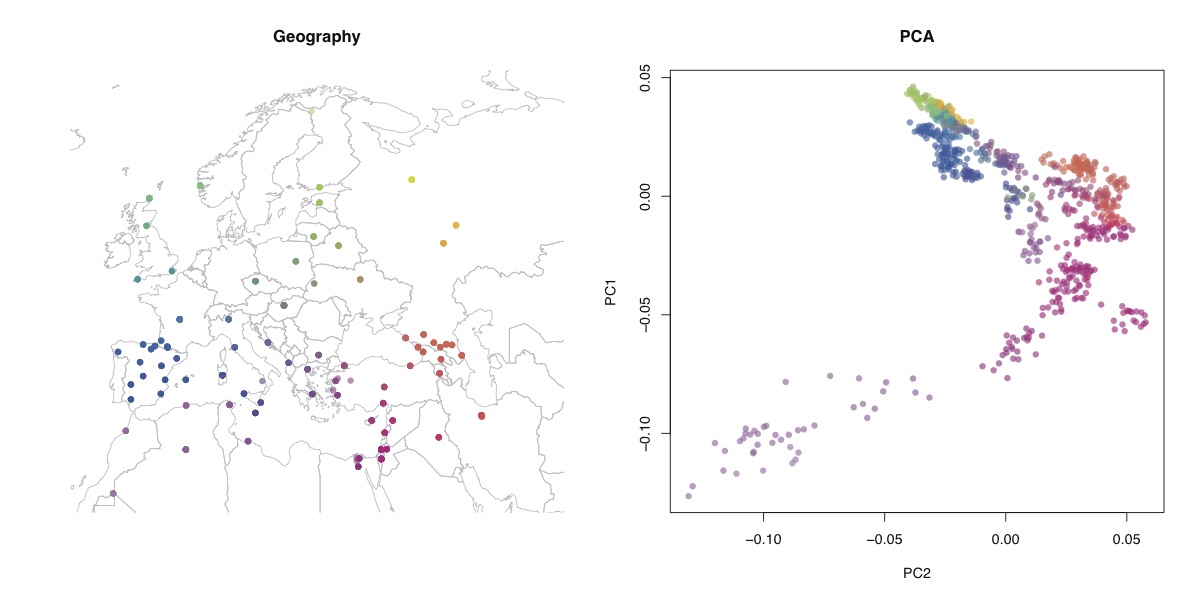
You can see that t-SNE clusters individual populations together much more tightly, but at the expense of preserving long-range structure. It certainly doesn’t look much like a map of Europe. Look how closely the Sardinians and Basques are clustered, but how far they are from each other. One advantage seems to be that it spreads out closely clustered populations - you can distinguish Orcadians and Czechs, whereas in PCA they’re all together. One thing that I can see this being very useful for is identifying cryptic relatedness in large homogenous samples - I’d like to see this run on the UK biobank, for example.